점과 선, 선과 선 사이의 거리

출처: http://mathworld.wolfram.com/Point-LineDistance2-Dimensional.html

1. 점과 선의 거리 (2D)

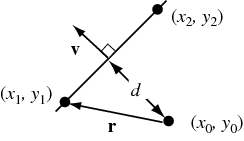
If the line is specified by two points and , then a vector perpendicular to the line is given by

(12)

Let be a vector from the point to the first point on the line

(13)

then the distance from to the line is again given by projecting onto , giving

2. 점과 선의 거리 (3D)

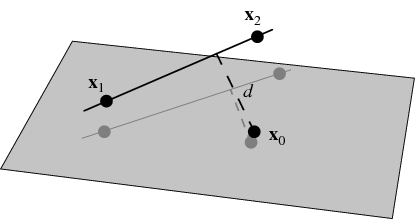
Let a line in three dimensions be specified by two points and lying on it, so a vector along the line is given by

(1)

The squared distance between a point on the line with parameter and a point is therefore

(2)

To minimize the distance, set and solve for to obtain

(3)

where denotes the dot product. The minimum distance can then be found by plugging back into (2) to obtain

	(4)
	(5)
	(6)

Using the vector quadruple product

(7)

where denotes the cross product then gives

(8)

and taking the square root results in the beautiful formula

			(9)
			(10)
			(11)

Here, the numerator is simply twice the area of the triangle formed by points , , and , and the denominator is the length of one of the bases of the triangle, which follows since, from the usual triangle area formula, .

CITE THIS AS:

Weisstein, Eric W. "Point-Line Distance--3-Dimensional." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html


3. 선과 선의 거리 (당연하지만 3D)

http://mathworld.wolfram.com/Line-LineDistance.html

Line-Line Distance

The distance between two skew lines with equations (1) (2) is given by (3) (Gellert et al. 1989, p. 538). This can be written in the concise form (4) by defining (5) (6) (7) SEE ALSO: Skew Lines, Line-Line Angle, Line-Line Intersection REFERENCES: Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989. Hill, F. S. Jr. "The Pleasures of 'Perp Dot' Products." Ch. II.5 in Graphics Gems IV (Ed. P. S. Heckbert). San Diego: Academic Press, pp. 138-148, 1994. CITE THIS AS: Weisstein, Eric W. "Line-Line Distance." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Line-LineDistance.html

[2011.10.26 즈음에 한 짓]

두 선 사이의 거리가 최소가 되는 점 X를 찾자.

syms x y z a1 b1 c1 a2 b2 c2 a3 b3 c3 a4 b4 c4;

X = [x y z];
X1 = [a1 b1 c1];
X2 = [a2 b2 c2];
X3 = [a3 b3 c3];
X4 = [a4 b4 c4];

d12 = sum((cross(X2-X1,X1-X)).^2)/sum((X2-X1).^2);
d34 = sum((cross(X4-X3,X3-X)).^2)/sum((X4-X3).^2);
d = d12 + d34;

dx = diff(d,x);
dy = diff(d,y);
dz = diff(d,z);

[x,y,z] = solve(dx,dy,dz, x,y,z)

test_lines03_result.txt