고정 헤더 영역
상세 컨텐츠
본문
1. 점과 선의 거리 (2D)
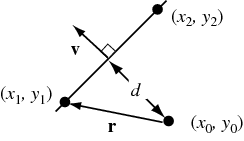
If the line is specified by two points ![]() and
and ![]() , then a vector perpendicular to the line is given by
, then a vector perpendicular to the line is given by
|
(12) |
Let ![]() be a vector from the point
be a vector from the point ![]() to the first point on the line
to the first point on the line
|
(13) |
then the distance from ![]() to the line is again given by projecting
to the line is again given by projecting ![]() onto
onto ![]() , giving
, giving
2. 점과 선의 거리 (3D)
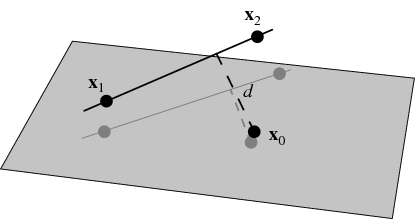
Let a line in three dimensions be specified by two points ![]() and
and ![]() lying on it, so a vector along the line is given by
lying on it, so a vector along the line is given by
![v=[x_1+(x_2-x_1)t; y_1+(y_2-y_1)t; z_1+(z_2-z_1)t].](http://mathworld.wolfram.com/images/equations/Point-LineDistance3-Dimensional/NumberedEquation1.gif) |
(1) |
The squared distance between a point on the line with parameter ![]() and a point
and a point ![]() is therefore
is therefore
|
(2) |
To minimize the distance, set ![]() and solve for
and solve for ![]() to obtain
to obtain
|
(3) |
where ![]() denotes the dot product. The minimum distance can then be found by plugging
denotes the dot product. The minimum distance can then be found by plugging ![]() back into (2) to obtain
back into (2) to obtain
|
(4) | |
|
(5) | |
|
(6) |
Using the vector quadruple product
|
(7) |
where ![]() denotes the cross product then gives
denotes the cross product then gives
|
(8) |
and taking the square root results in the beautiful formula
|
(9) | |||
|
(10) | |||
|
(11) |
Here, the numerator is simply twice the area of the triangle formed by points ![]() ,
, ![]() , and
, and ![]() , and the denominator is the length of one of the bases of the triangle, which follows since, from the usual triangle area formula,
, and the denominator is the length of one of the bases of the triangle, which follows since, from the usual triangle area formula, ![]() .
.
CITE THIS AS:
Weisstein, Eric W. "Point-Line Distance--3-Dimensional." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html
3. 선과 선의 거리 (당연하지만 3D)
http://mathworld.wolfram.com/Line-LineDistance.html
| ||||||||||||||||||||||||
|
The distance between two skew lines with equations
is given by
(Gellert et al. 1989, p. 538). This can be written in the concise form
by defining
Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989. Hill, F. S. Jr. "The Pleasures of 'Perp Dot' Products." Ch. II.5 in Graphics Gems IV (Ed. P. S. Heckbert). San Diego: Academic Press, pp. 138-148, 1994. CITE THIS AS: Weisstein, Eric W. "Line-Line Distance." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Line-LineDistance.html |
[2011.10.26 즈음에 한 짓]
두 선 사이의 거리가 최소가 되는 점 X를 찾자.
X1 = [a1 b1 c1];
X2 = [a2 b2 c2];
X3 = [a3 b3 c3];
X4 = [a4 b4 c4];
d34 = sum((cross(X4-X3,X3-X)).^2)/sum((X4-X3).^2);
d = d12 + d34;
dy = diff(d,y);
dz = diff(d,z);
[x,y,z] = solve(dx,dy,dz, x,y,z)
 test_lines03_result.txt
test_lines03_result.txt



